六边形网格

这篇文章覆盖了制作六边形地图所涉及到相关的方法，通用公式和算法。为了文章更加优雅简洁，文中的实例都将使用伪代码进行描述。

几何性质

六边形是由六个边组成的。正六边形的每条边长度相同。我们这里假设所有的六边形都是正六边形。六边形的方向有两个： 1. 垂直列方向(六边形的任意两条平行边在垂直方向上)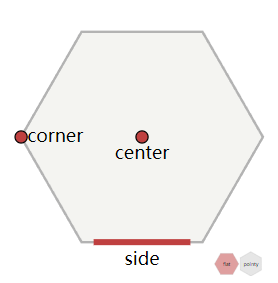

2. 水平行反向(六边形的任意两条平行边在水平方向上)

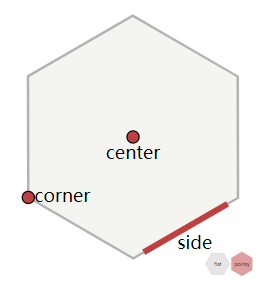
六边形有6个边和6个角。每个边被两个六边形共享。每个角被三个六边形共享。更多关于中心点(centers), 边(sides), 和 角(corners)可以参见这篇文章（四边形，六边性和三角形）。

角度

一个正六边的内角是\(120^°\)。有六个“楔形”，每个都是一个内角为\(60^°\)的等边三角形。每个角到中心的距离相等定义为它的大小。 使用以下代码去绘制一个六边形：

function pointy_hex_corner(center, size, i):
    var angle_deg = 60 * i //垂直方向
    //var angle_deg = 60 * i - 30°//水平方向
    var angle_rad = PI / 180 * angle_deg
    return Point(center.x + size * cos(angle_rad),
                 center.y + size * sin(angle_rad))

通过pointy_hex_corner(..., 0) 到pointy_hex_corner(..., 5)分别计算出六边形的6个顶点。然后绘制线连接各个顶点，则形成了六边形的外框了。

两个不同方向的六边形的角度是不一样的。 1. 垂直方向的角度是：\(0^°\)，\(60^°\)，\(120^°\)，\(180^°\)，\(240^°\)，\(300^°\)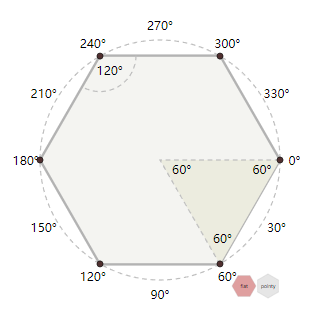

2. 水平方向的角度是：\(30^°\)，\(90^°\)，\(150^°\)，\(210^°\)，\(270^°\)，\(330^°\)

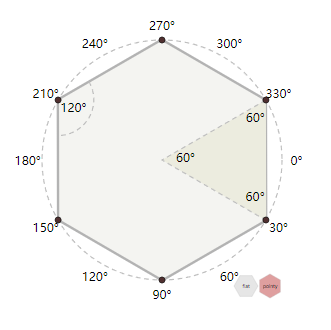
说明：图中的y轴向下，角度的正方向是顺时针的。如果你y轴是向上的，角度的正方向是逆时针的，则需要做相应的调整。

在数学上，六边形的外接圆半径就是从中心到顶点的距离，我们称之为六边形的大小；内接圆半径是从中心点到边的距离。“最大直径”是外接圆半径的两倍，“最小直径”是内接圆半径的两倍。

大小(size)和间距(Spacing)

现在我们将多个六边形放在一起。其中size被定义为从中心点到任意角的距离。 1. 在垂直方向上(平直边平行于水平轴)，六边形的宽w = 2 * size, 高h = \(2 * \frac{\sqrt{3}}{2} * size\) = \(\sqrt{3} * size\)(其中\(\sqrt{3}\)是根据\(sin(60^°)\)而来)。两个相邻六边形中心点水平之间的距离被定义为水平间距（horizontal spacing）= \(w * \frac{3}{4}\), 两中心点垂直方向的间距被定义为垂直间距（vertical spacing）= h。如下图：

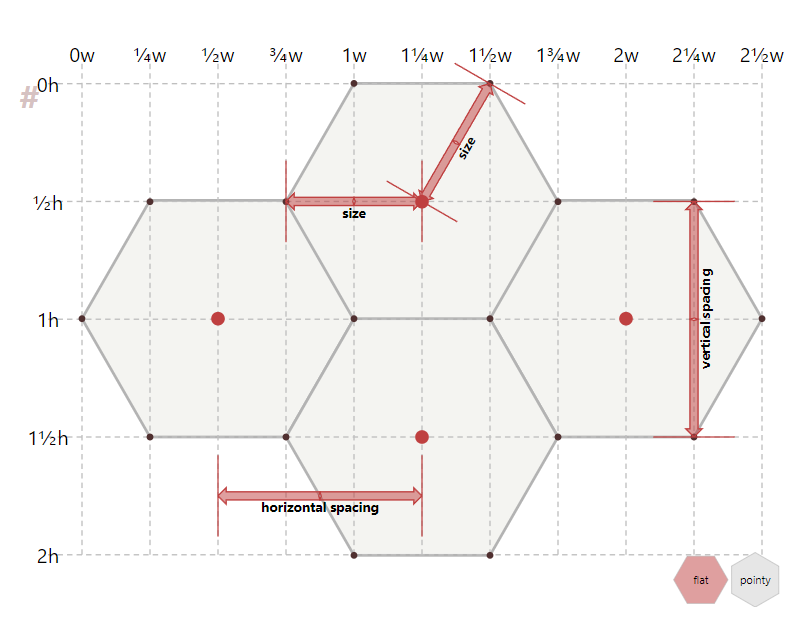
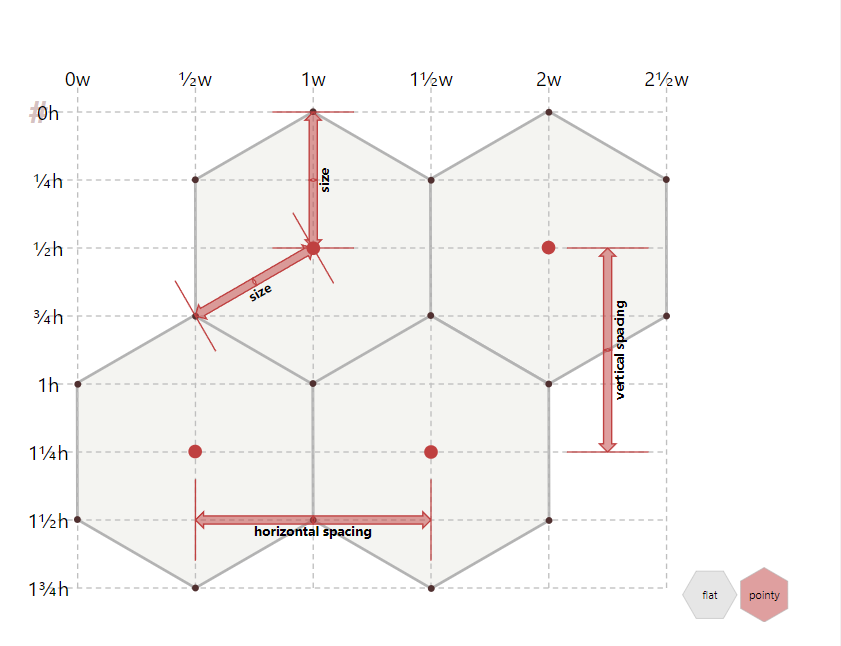
2. 在水平方向上(平直边平行于垂直轴)，六边形的宽w = \(\sqrt{3} * size\),高h = 2 * size。两个相邻六边形中心点水平之间的距离被定义为水平间距（horizontal spacing）= w, 两中心点垂直方向的间距被定义为垂直间距（vertical spacing）= \(h * \frac{3}{4}\)

一些游戏使用像素风格可能导像素数不能匹配到真实的正多边形上。在这个章节描述角度和间距可能不能够匹配到你的六边形大小。这篇文章的其余部分描述了六边形在六边形网格上的算法，即使你的六边形被拉伸或收缩了一点，我也会在这篇文章说明如何处理拉伸。

坐标系统

现在我们将六边形组装成一个网格。 对于方形网格，方法就比较明显了，可以将六边形逐行拼接即可。 对于六边形来说，有多种方法。我喜欢用于算法的立方体坐标（Cube coordinates）和轴向坐标（Axial coordinates）或用于存储的双倍坐标（Doubled coordinates）。

偏移坐标（Offset coordinates）

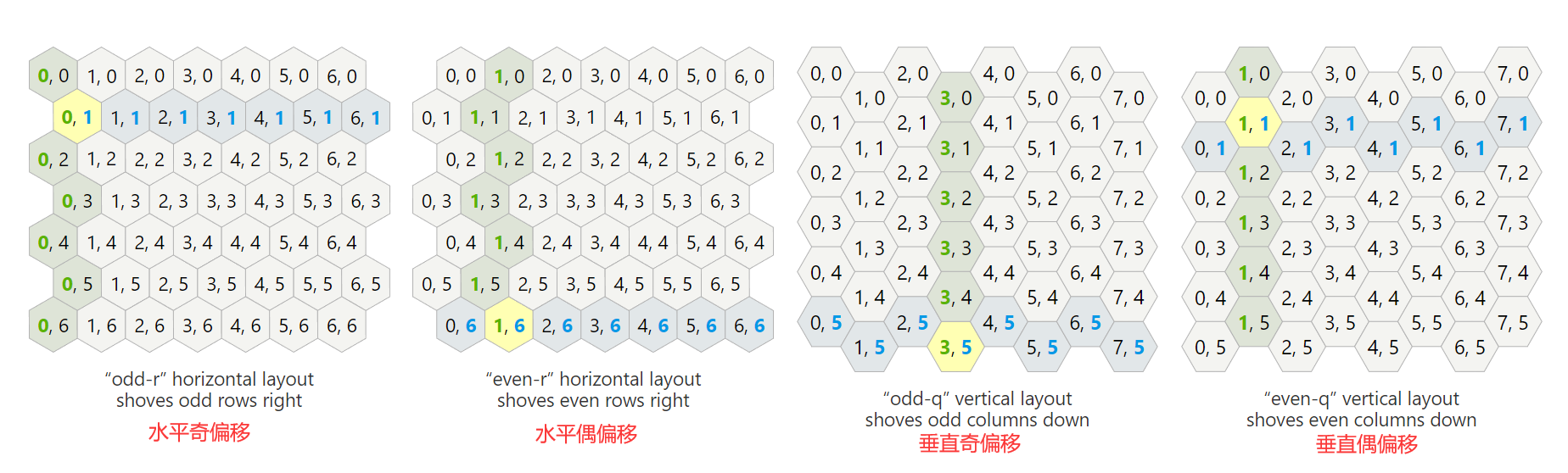
偏移坐标是将正六变形在每一列或行进行偏移组成的一个网格，列被命名为col(q), 行被命名为row(r)。我们可以选择偏移奇或偶（列/行），所以在水平或垂直方向上又有两种变体（奇偏移或偶偏移）。如下图：

立方体坐标（Cube coordinates）

另一种观察六边形网格的方式是六边形定义有三个轴，不像偏移坐标这种只有两个轴的方形网格，立方体坐标多了一些对称美。 让我们取一个立方体网格并在x + y + z = 0的位置切出一个对角平面。如下图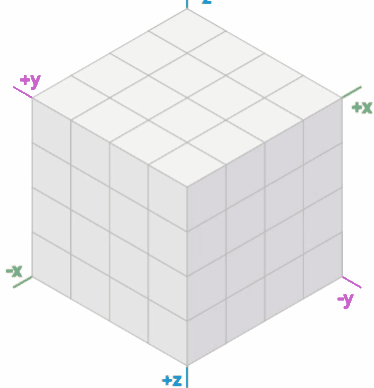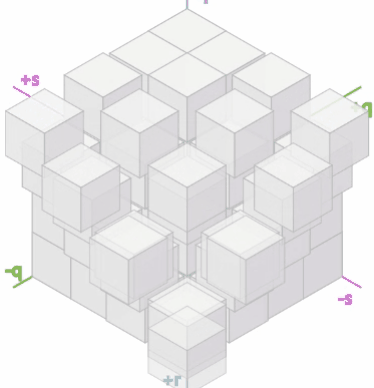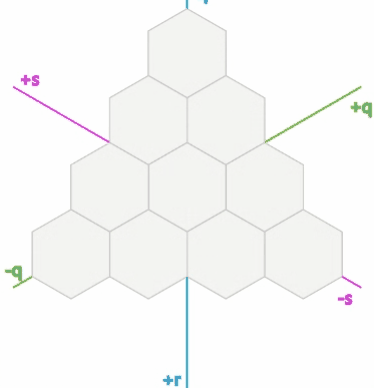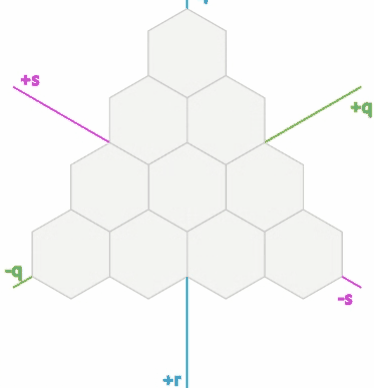： 这虽然是个奇怪的想法，但它可以帮助我们使用六边形网格算法： 1. 在3D笛卡尔积坐标系中，有一些标准的向量操作：加或减，乘或除等运算。我们能在六边形网格中使用这些操作。偏移坐标不支持这些操作。 2. 在3D笛卡尔积坐标系中，有一些现存的算法，比如：距离，旋转，反射，绘线，转换坐标等。这些算法也是适用于六边形网格。

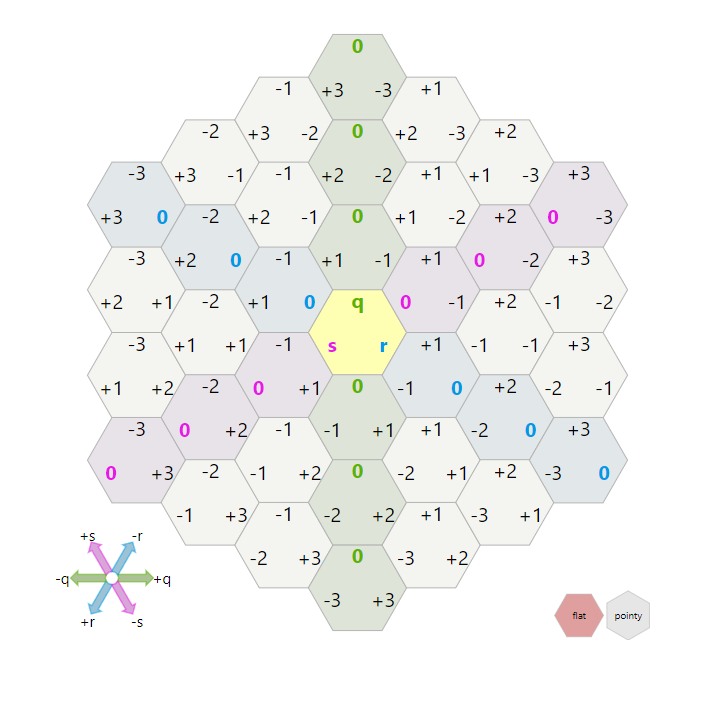立方体坐标是六边形网格坐标系的合理选择。强制约束q + r + s = 0，所以算法必须保证这一约束。该约束还确保每个六边形都有一个规范坐标（q+r+s=0）。

轴向坐标（Axial coordinates）

轴向坐标和立方体坐标是相同的，轴向坐标中我们不用存储s轴坐标的值，因为我们限制q+r+s=0, 当我们需要s时，可以通过s=-q-r得到。 轴向/立方体坐标，允许在六边形网格中使用加，减，乘和除。偏移坐标不允许这样做，这使得使用轴向/立方体坐标在算法使用上更简单。

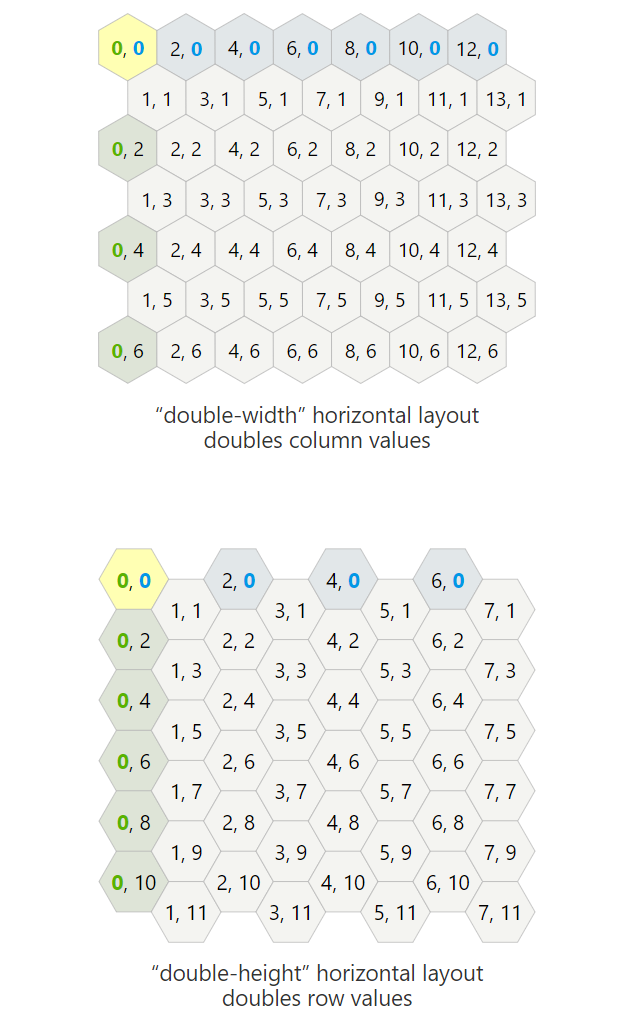
双倍坐标（Doubled coordinates）

虽然我推荐使用轴向坐标（Axial coordinates）和立方体坐标（Cube coordinates）,如果你还是执意于偏移坐标（Offset coordinates），那么可以考虑的它的另一种形式即双倍坐标（Doubled coordinates）。它能确保大部分的算法更加容易实现。双倍坐标不是交替，而是水平或垂直步长是偏移坐标的两倍。它有个限制即：(col+row)%2==0。在水平（尖顶在上）布局中，每个六边形将列增加2；在垂直（平顶在上）布局中，每个六边形将行增加2。这允许介于两者之间的六边形使用中间值。如图：

推荐

推荐什么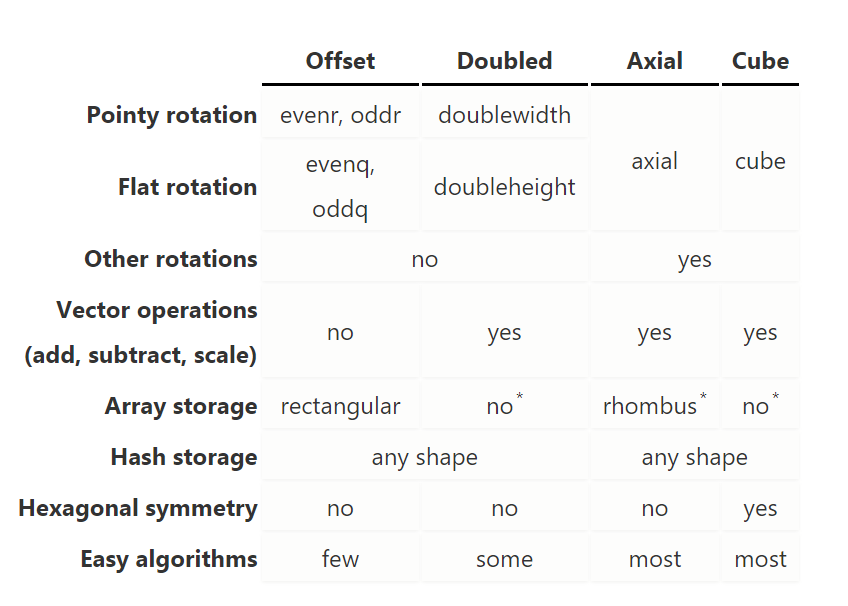？ 我推荐：如果你仅打算使用没有旋转的矩形地图，考虑使用双倍坐标（Doubled coordinates）或偏移坐标（Offset coordinates）。对于有旋转或非矩形形状的地图使用轴向坐标（Axial coordinates）或立方体坐标（Cube coordinates）。对于立方体坐标你可以选择存储s（立方体坐标）或在需要时通过-q-r计算得到（轴向坐标）。

坐标转换

您可能会在项目中使用轴向或偏移坐标，但许多算法更容易以轴向/立方体坐标表示。 因此，您需要能够来回转换。

轴向坐标

轴向和立方体坐标本质上是相同的。在立方体坐标统中，我们存储第三个轴，s。在轴向坐标统中，我们不存储它，但在我们需要时不得不通过，s=-q-r进行计算。

function cube_to_axial(cube):
    var q = cube.q
    var r = cube.r
    return Hex(q,r)

function axial_to_cube(hex):
    var q = hex.q
    var r = hex.r
    var s = -q-r
    return Cube(q, r, s)

偏移坐标

偏移坐标转换，首先需要确定使用的是-r（尖顶在上）还是-q（平顶在上）。这两种坐标系的转换是不同的：

// axial from/to oddr
function axial_to_oddr(hex):
    var col = hex.q + (hex.r - (hex.r & 1)) / 2
    var row = hex.r
    return OffsetCoord(col, row)

function oddr_to_axial(hex):
    var q = hex.col - (hex.row - (hex.row & 1)) / 2
    var r = hex.row
    return Hex(q,r)
// axial from/to evenr
function axial_to_evenr(hex):
    var col = hex.q + (hex.r - (hex.r & 1)) / 2
    var row = hex.r
    return OffsetCoord(col, row)

function evenr_to_axial(hex):
    var q = hex.col - (hex.row - (hex.row & 1)) / 2
    var r = hex.row
    return Hex(q,r)

// axial from/to oddq
function axial_to_oddq(hex):
    var col = hex.q
    var row = hex.r + (hex.q - (hex.q&1)) / 2
    return OffsetCoord(col, row)

function oddq_to_axial(hex):
    var q = hex.col
    var r = hex.row - (hex.col - (hex.col&1)) / 2
    return Hex(q, r)

// axial from/to evenq
function axial_to_evenq(hex):
    var col = hex.q
    var row = hex.r + (hex.q + (hex.q&1)) / 2
    return OffsetCoord(col, row)

function evenq_to_axial(hex):
    var q = hex.col
    var r = hex.row - (hex.col + (hex.col&1)) / 2
    return Hex(q, r)

上述代码中使用了位运算&对2进行求模运算

双倍坐标

function doubleheight_to_axial(hex):
    var q = hex.col
    var r = (hex.row - hex.col) / 2
    return Hex(q, r)

function axial_to_doubleheight(hex):
    var col = hex.q
    var row = 2 * hex.r + hex.q
    return DoubledCoord(col, row)

function doublewidth_to_axial(hex):
    var q = (hex.col - hex.row) / 2
    var r = hex.row
    return Hex(q, r)

function axial_to_doublewidth(hex):
    var col = 2 * hex.q + hex.r
    var row = hex.r
    return DoubledCoord(col, row)

如果你使用的是立方体坐标，使用立方体坐标Cube（q, r, -q-r）代替轴向坐标Hex(q, r)。

相邻六边形（Neighbors）

给定一个六边形，哪6个六边形与它相邻？ 如您所料，立方体坐标的答案是最简单的，轴向坐标仍然非常简单，而偏移坐标则稍微复杂一些。我们可能还想计算6个“对角线”六边形。

立方体坐标

在六边形坐标中移动一个格子涉及改变立方体坐标中3个分量中的其中一个+1且另一个-1（必须保证和为0）。立方体坐标中3个轴都有可能+1，剩下的2个轴可能-1。在相邻的6个六边形中，每个相当于六边形的6个方向。最简单和最快速的方法是预先计算存储它们在一个表中：

var cube_direction_vectors = [
    Cube(+1, 0, -1), Cube(+1, -1, 0), Cube(0, -1, +1), 
    Cube(-1, 0, +1), Cube(-1, +1, 0), Cube(0, +1, -1), 
]

function cube_direction(direction):
    return cube_direction_vectors[direction]

function cube_add(hex, vec):
    return Cube(hex.q + vec.q, hex.r + vec.q, hex.s + vec.s)

function cube_neighbor(cube, direction):
    return cube_add(cube, cube_direction(direction))

使用立方体坐标系统，我们能存储不同两个不同的坐标值为一个“向量”，并且这些坐标可以相加得到另外一个坐标。这就是cube_add函数所做的功能。轴坐标和双倍坐标也支持此运算，但偏移坐标不支持。

轴坐标

轴坐标除了不存储第三个坐标以外，其他的和立方体坐标是相同的。代码除了不写第三个轴外，其他的都和立方体坐标相同：

var cube_direction_vectors = [
    Cube(+1, 0), Cube(+1, -1), Cube(0, -1), 
    Cube(-1, 0), Cube(-1, +1), Cube(0, +1), 
]

function cube_direction(direction):
    return cube_direction_vectors[direction]

function cube_add(hex, vec):
    return Cube(hex.q + vec.q, hex.r + vec.q)

function cube_neighbor(cube, direction):
    return cube_add(cube, cube_direction(direction))

偏移坐标

与立方体和轴坐标一样，我们将构建一个需要添加到 col 和 row 的数字的表格。然而偏移坐标系不能够安全的进行加减。例如，从 (0, 0) 向东南移动会将我们带到 (0, +1)，因此我们可以将 (0, +1) 放入表中以向东南移动。 但是从 (0, +1) 向东南移动会将我们带到 (+1, +2)，因此我们需要将 (+1, +1) 放入该表中。需要添加的数量依赖我们在表格中的位置。 因此偏移坐标对于奇和偶列/行是有区别的，我们需要分两个列表来存储邻接六边形列表。

// odd-r
var oddr_direction_differences = [
    // even rows 
    [[+1,  0], [ 0, -1], [-1, -1], 
     [-1,  0], [-1, +1], [ 0, +1]],
    // odd rows 
    [[+1,  0], [+1, -1], [ 0, -1], 
     [-1,  0], [ 0, +1], [+1, +1]],
]

function oddr_offset_neighbor(hex, direction):
    var parity = hex.row & 1
    var diff = oddr_direction_differences[parity][direction]
    return OffsetCoord(hex.col + diff[0], hex.row + diff[1])

// even-r
var evenr_direction_differences = [
    // even rows 
    [[+1,  0], [+1, -1], [ 0, -1], 
     [-1,  0], [ 0, +1], [+1, +1]],
    // odd rows 
    [[+1,  0], [ 0, -1], [-1, -1], 
     [-1,  0], [-1, +1], [ 0, +1]],
]

function evenr_offset_neighbor(hex, direction):
    var parity = hex.row & 1
    var diff = evenr_direction_differences[parity][direction]
    return OffsetCoord(hex.col + diff[0], hex.row + diff[1])

// odd-q
var oddq_direction_differences = [
    // even cols 
    [[+1,  0], [+1, -1], [ 0, -1], 
     [-1, -1], [-1,  0], [ 0, +1]],
    // odd cols 
    [[+1, +1], [+1,  0], [ 0, -1], 
     [-1,  0], [-1, +1], [ 0, +1]],
]

function oddq_offset_neighbor(hex, direction):
    var parity = hex.col & 1
    var diff = oddq_direction_differences[parity][direction]
    return OffsetCoord(hex.col + diff[0], hex.row + diff[1])

// even-q
var evenq_direction_differences = [
    // even cols 
    [[+1, +1], [+1,  0], [ 0, -1], 
     [-1,  0], [-1, +1], [ 0, +1]],
    // odd cols 
    [[+1,  0], [+1, -1], [ 0, -1], 
     [-1, -1], [-1,  0], [ 0, +1]],
]

function evenq_offset_neighbor(hex, direction):
    var parity = hex.col & 1
    var diff = evenq_direction_differences[parity][direction]
    return OffsetCoord(hex.col + diff[0], hex.row + diff[1])

双倍坐标

不像偏移坐标，双倍坐标的邻接六边形不依赖于我们使用的是列/行。它们在任何地方都是相同的，与轴向/立方体坐标。同样与偏移坐标不同，我们可以安全地减去和添加双倍坐标，这使得它们比偏移坐标更容易使用。

// double width
var doublewidth_direction_vectors = [
    DoubledCoord(+2,  0), DoubledCoord(+1, -1), 
    DoubledCoord(-1, -1), DoubledCoord(-2,  0), 
    DoubledCoord(-1, +1), DoubledCoord(+1, +1), 
]

function doublewidth_add(hex, diff):
    return DoubleCoord(hex.col + diff.col, hex.row + diff.row)

function doublewidth_neighbor(hex, direction):
    var vec = doublewidth_direction_vectors[direction]
    return doublewidth_add(hex, vec)

// double height 
var doubleheight_direction_vectors = [
    DoubledCoord(+1, +1), DoubledCoord(+1, -1), 
    DoubledCoord( 0, -2), DoubledCoord(-1, -1), 
    DoubledCoord(-1, +1), DoubledCoord( 0, +2), 
]

function doubleheight_add(hex, diff):
    return DoubleCoord(hex.col + diff.col, hex.row + diff.row)

function doubleheight_neighbor(hex, direction):
    var vec = doubleheight_direction_vectors[direction]
    return doubleheight_add(hex, vec)

对角线

移动到六边形坐标中的“对角线”空间会使 3 个立方体坐标中的一个改变 ±2，另外两个改变 ∓1（总和必须保持为 0）。

var cube_diagonal_vectors = [
    Cube(+2, -1, -1), Cube(+1, -2, +1), Cube(-1, -1, +2), 
    Cube(-2, +1, +1), Cube(-1, +2, -1), Cube(+1, +1, -2), 
]

function cube_diagonal_neighbor(cube, direction):
    return cube_add(cube, cube_diagonal_vectors[direction])

距离

立方体坐标

由于六边形立方体坐标是基于3D立方体坐标的，所以我们在六边形网格中也能适用于3D中的距离计算。每个六边形网格相当于3D空间中的一个立方体。在六边形网格中，邻接六边形的距离是1但在立方体网格中其距离是2。对于在立方体网格中步长为2的，在六边形形网格中步长则为1。在3D立方体网格中，经典的曼哈顿距离是abs(dx)+abs(dy)+abs(dz)，那么在六边形网格中的距离则是它的一半。

function cube_subtract(a, b):
    return Cube(a.q - b.q, a.r - b.r, a.s - b.s)

function cube_distance(a, b):
    var vec = cube_subtract(a, b)
    return (abs(vec.q) + abs(vec.r) + abs(vec.s)) / 2
    // or: (abs(a.q - b.q) + abs(a.r - b.r) + abs(a.s - b.s)) / 2

我们注意三个坐标中的一个必须是其他两个坐标的总和，然后选择这个作为距离。这也是一种计算距离等效的方法，您可能更喜欢上面的“除以二”形式，或者这里的“最大”形式，但它们给出的结果相同：

function cube_subtract(a, b):
    return Cube(a.q - b.q, a.r - b.r, a.s - b.s)

function cube_distance(a, b):
    var vec = cube_subtract(a, b)
    return max(abs(vec.q), abs(vec.r), abs(vec.s))
    // or: max(abs(a.q - b.q), abs(a.r - b.r), abs(a.s - b.s))

距离

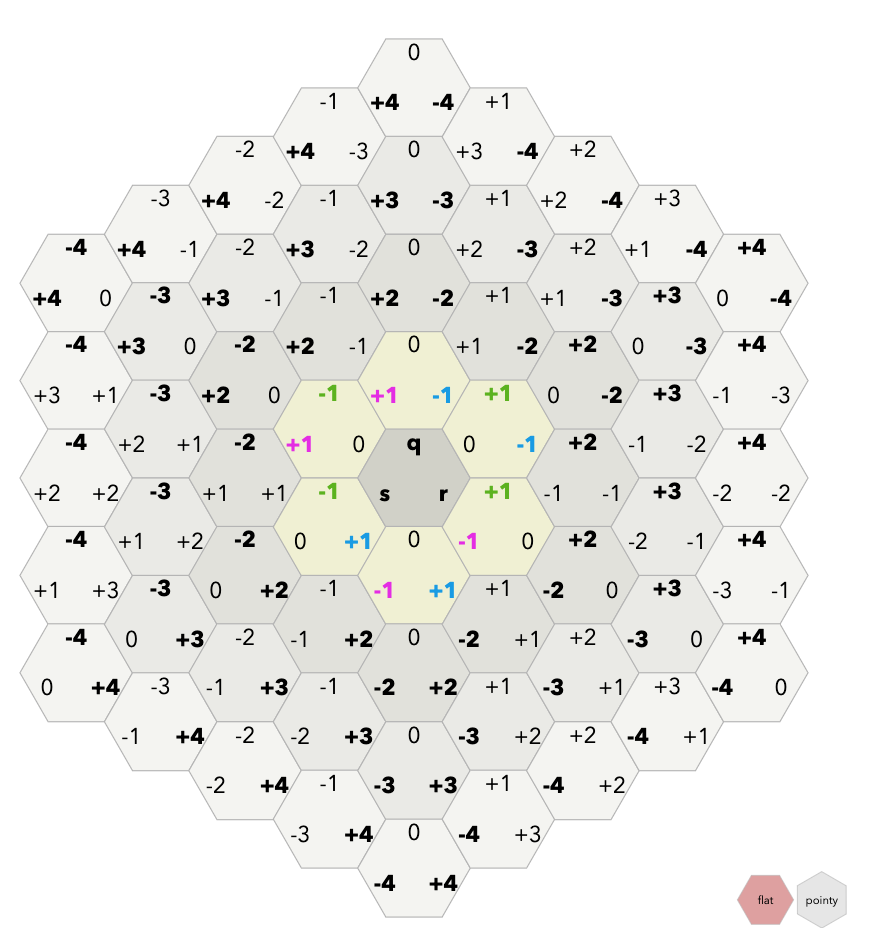
轴坐标

在轴的系统中，第三个轴是隐式的。我们总是能够转换一个轴坐标到立方体坐标去计算距离：

function axial_distance(a, b):
    var ac = axial_to_cube(a)
    var bc = axial_to_cube(b)
    return cube_distance(ac, bc)

一旦我们内联这些函数，结果将如下：

function axial_distance(a, b):
    return (abs(a.q - b.q) 
          + abs(a.q + a.r - b.q - b.r)
          + abs(a.r - b.r)) / 2

上面的形式也能被写成：

function axial_subtract(a, b):
    return Hex(a.q - b.q, a.r - b.r)

function axial_distance(a, b):
    var vec = axial_subtract(a, b)
    return (abs(vec.q)
          + abs(vec.q + vec.r)
          + abs(vec.r)) / 2

偏移坐标

与轴坐标一样，我们将转换偏移坐标到轴/立方体坐标，然后使用轴/立方坐标的计算方法。

function offset_distance(a, b):
    var ac = offset_to_axial(a)
    var bc = offset_to_axial(b)
    return axial_distance(ac, bc)

我们将使用相同的模式对于大多数的算法：转换偏移到轴/立方体坐标，然后应用的轴/立方体坐标的算法，并转换任意的轴/立方体坐标的结果回偏移坐标。

双倍坐标

虽然转换双倍坐标到轴/立方体坐标也是可行的，但是在rot.js手册中，有直接的距离计算公式：

function doublewidth_distance(a, b):
    var dcol = abs(a.col - b.col)
    var drow = abs(a.row - b.row)
    return drow + max(0, (dcol-drow)/2)

function doubleheight_distance(a, b):
    var dcol = abs(a.col - b.col)
    var drow = abs(a.row - b.row)
    return dcol + max(0, (drow−dcol)/2)

绘线

如何去绘制一条从一个六边形格子到另一个六边形格子的线呢？我使用线性插值来绘制线条。在N+1个点上均匀地对线进行采样，并且查找出这些采样点对应的六边形格子。 1. 首先我们计算N=x为端点的六边形网格距离。 2. 然后均匀的在点A和点B之间进行N+1点的采样。使用线性插值，每个点将是A+(B-A)1.0/N i，值i从0到N。这采样的结果点坐标是浮点型的。 3. 转换浮点型的坐标到六边形的整形坐标。这个算法被叫做cube_round。

将上面步骤整合后绘制一条从A到B的线。

function lerp(a, b, t): // for floats
    return a + (b - a) * t

function cube_lerp(a, b, t): // for hexes
    return Cube(lerp(a.q, b.q, t),
                lerp(a.r, b.r, t),
                lerp(a.s, b.s, t))

function cube_linedraw(a, b):
    var N = cube_distance(a, b)
    var results = []
    for each 0 ≤ i ≤ N:
        results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
    return results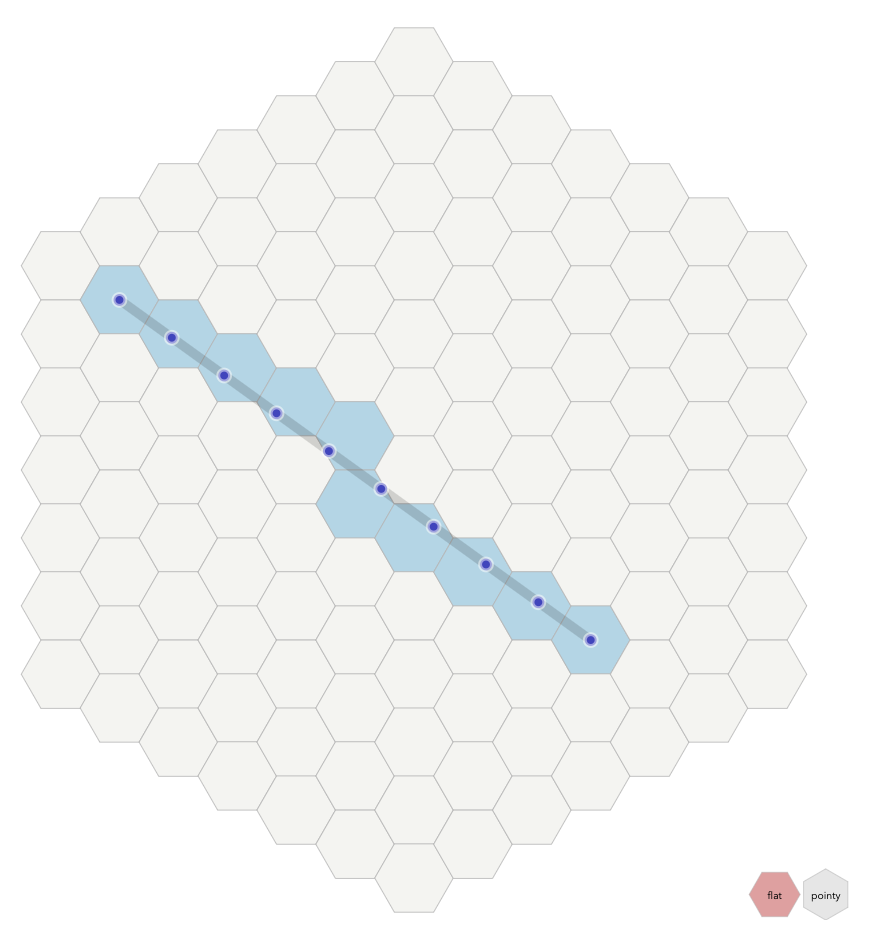

移动范围

坐标范围

给定一个六边形中心和和范围N, 哪些六边形在距离它的N步内？我们依据前面讲解的距离公式，distance=max(abs(q),abs(r), abs(s)),去查找都在N范围内的六边形，我们需要max(abs(q),abs(r), abs(s)) <= N。这意味着需要满足\(abs(q)\le N，abs(r)<=N\)以及\(abs(s)\le N\)。移除绝对值符号，我们将得到\(-N \le q \le +N\), \(-N \le r \le +N\)以及\(-N \le s \le +N\)

var results = []
for each -N ≤ q ≤ +N:
    for each -N ≤ r ≤ +N:
        for each -N ≤ s ≤ +N:
            if q + r + s == 0:
                results.append(cube_add(center, Cube(q, r, s)))

这个循环是能够正常运行的，但是有些低效。s的所有值循环完后只有一个满足q+r+s=0的限制。我们可以直接计算满足限制的s的值：

var results = []
for each -N ≤ q ≤ +N:
    for each max(-N, -q-N) ≤ r ≤ min(+N, -q+N):
        var s = -q-r
        results.append(cube_add(center, Cube(q, r, s)))

这个循环迭代完确切需要的坐标。在图中，每个范围都是一对线。 每条线都是一个不等式（半平面）。我们选择满足所有六个不等式的所有六边形。这个循环在轴坐标中也有效：

var results = []
for each -N ≤ q ≤ +N:
    for each max(-N, -q-N) ≤ r ≤ min(+N, -q+N):
        results.append(axial_add(center, Hex(q, r)))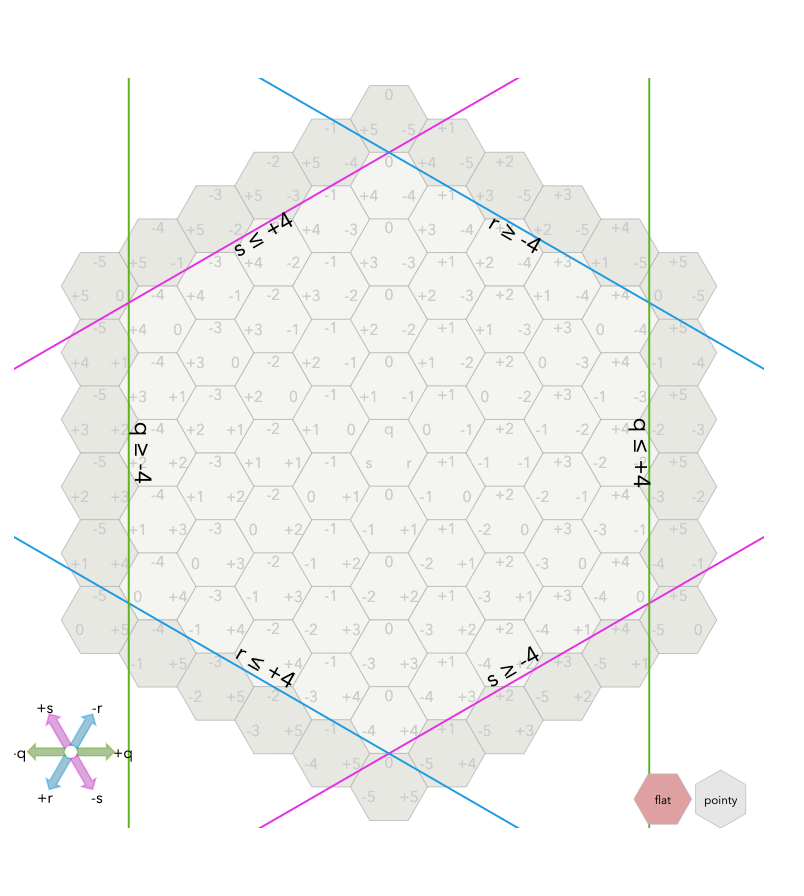

相交范围

如果你要查找多个范围的六边形，你能在产生一个六边形列表前将这些范围相交。 你可以用代数和几何方法来思路这个问题。 代数，每个六边形范围可以用一个不等\(-N \le dq \le +N\)表示，并且我们将解决这些约束的交集。 几何，在3D空间中，每个范围是一个立方体，并且我们准备在3D空间中让这两个立方体相交。然后投影回q+r+s=0的平面去获得对应的六边形。我们打算使用代数方式去解决相交的问题： 首先，我们重写\(-N \le dq \le +N\)限制为一般形式，\(q_{min} \le q \le q_{max}\) 并且设置q_{min} = center.q-N，q_{max} = center.q+N。对于r和s也是一样，最后从上一节的代码中概括得到：

var results = []
for each $q_{min}$ ≤ q ≤ $q_{max}$:
    for each max($r_{min}$, -q-$s_{max}$) ≤ r ≤ min($r_{max}$, -q-$s_{min}$):
        results.append(Hex(q, r))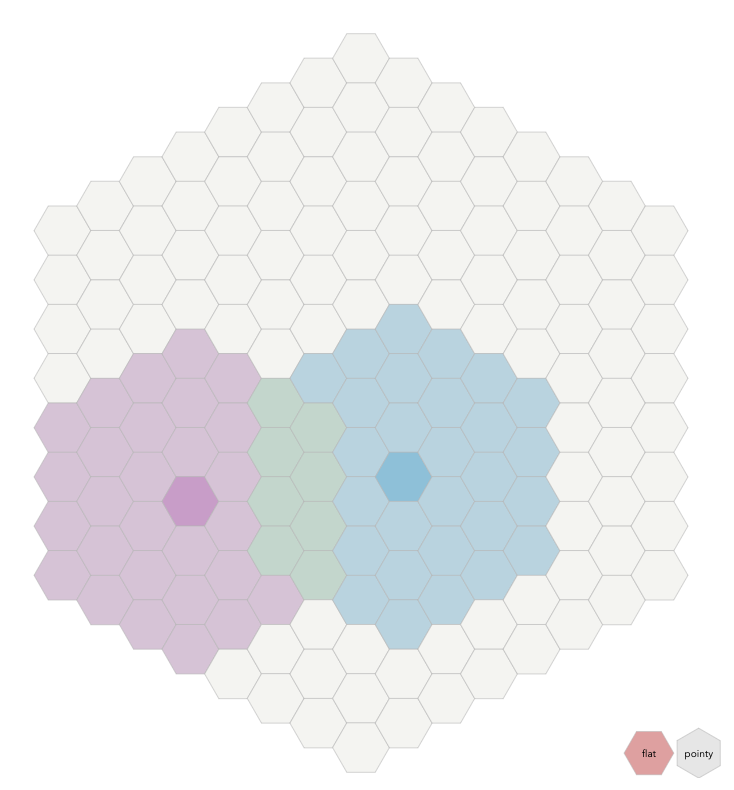

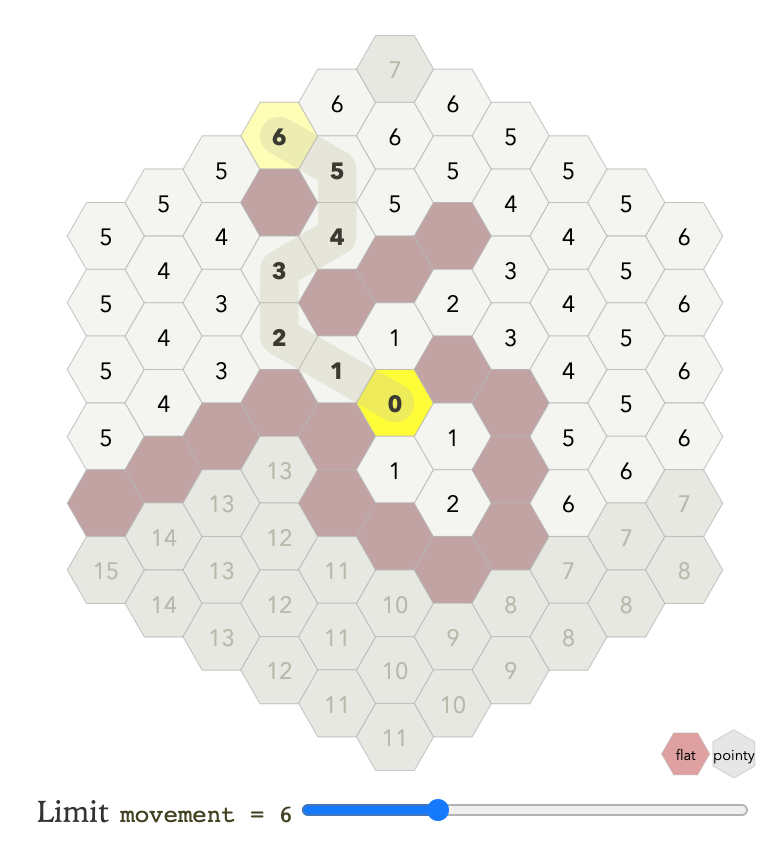
两个范围\(a \le q \le b\)和\(c \le q \le d\)相交得\(max(a,c) \le q \le min(b, d)\)。由于六边形区域表示为 q, r, s 上的范围，我们可以分别与 q, r, s 范围中的每一个相交，然后使用嵌套循环在相交处生成六边形列表。对于一个六边形区域，我们设置 \(q_{min} = H.q - N\) 和 \(q_{max} = H.q + N\) 并且对于 r 和 s 也是如此。 对于相交的两个六边形区域，我们设置 \(q_{min} = max(H1.q - N, H2.q - N)\) 和 \(q_{max} = min(H1.q + N, H2.q + N)\)，对于 r 和 s 也是如此。这样的模式对于多个区域也是有效的，并且能够泛化到其他的形状（三角形，梯形，菱形和不规则的六边形）。

障碍

如果有障碍物，最简单的做法是有限距离的洪水填充（flood fill）（广度优先搜索）。 在此图中，限制设置为移动。 在代码中， fringes[k] 是可以在 k 步内到达的所有六边形的数组。 每次通过主循环，我们将级别 k-1 扩展为级别 k。 这同样适用于任何六边形坐标系（立方体、轴向、偏移、加倍）。

function hex_reachable(start, movement):
    var visited = set() # set of hexes
    add start to visited
    var fringes = [] # array of arrays of hexes
    fringes.append([start])

    for each 1 < k ≤ movement:
        fringes.append([])
        for each hex in fringes[k-1]:
            for each 0 ≤ dir < 6:
                var neighbor = hex_neighbor(hex, dir)
                if neighbor not in visited and not blocked:
                    add neighbor to visited
                    fringes[k].append(neighbor)

    return visited